Метод Делаира или метод латинских квадратов
Суть метода
1. Из целых чисел от 0 до n-1 строятся два латинских квадрата размерности n x n.
Первая строка первого квадрата строится следующим образом:
На первое место ставится число (n-1)/2, остальные числа занимают произвольные позиции.
Каждая следующая строка строится из предыдущей, переносом каждого элемента на единицу вправо.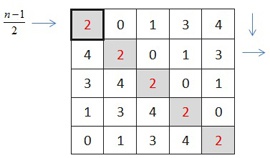
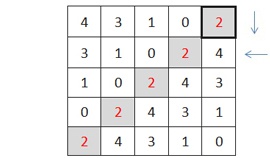
Второй квадрат строится аналогично, только:
Число (n-1)/2 ставиться на последнее место в первой строке.
Каждая следующая строка строится из предыдущей переносом каждого элемента на единицу влево.
Каждый элемент первого квадрата умножается на n, а к каждому элементу второго квадрата прибавляется 1.
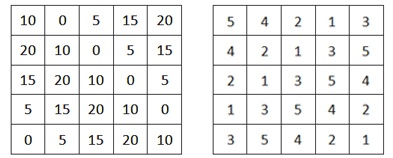
Затем, каждый элемент первого квадрата складывается с соответствующим ему элементом второго квадрата.
В результате получается магический квадрат, заполненный числами от 1 до n^2.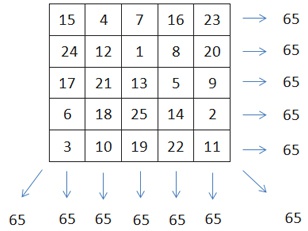
Реализация на Python
1. Задается матрица, которая будет содержать первый латинский квадрат. И заполняется элементами от 0 до n-1
import numpy
n=input('Please enter n: ')
A=numpy.zeros([n,n])
for i in range(n):
A[i][i]=(n-1)/2
for k in range(n):
if k<(n-1)/2:
if i+k+1<n:
A[i][i+k+1]=k
else:
A[i][i+k+1-n]=k
else:
if k==(n-1)/2:
pass
else:
if k+i<n:
A[i][i+k]=k
else:
A[i][i+k-n]=k
2. Затем, задается вторая матрица, которая будет содержать магический квадрат.
Каждый элемент магического квадрата будет получаться путем умножения соответствующего элемента первой матрицы на n, прибавления к результату умножения элемента с позицией n-1-k (где k — позиция нужного элемента той же строки) и прибавления к результату 1.
B=numpy.zeros([n,n])
for i in range(n):
for k in range(n):
B[i][k]=A[i][k]*n+A[i][n-1-k]+1
