При численном решении этой задачи методом конечных разностей отрезок [a,b] разбивают на равные части с шагом h точками x i , где h=(b−a)/n.



Заменяя производные правыми односторонними конечно — разностными отношениями для внутренних точек x i и концевых точек отрезка [a,b], и выполняя алгебраические преобразования, получим систему линейных алгебраических уравнений

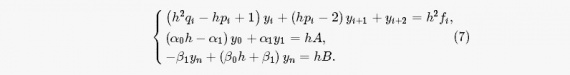
Реализовать решение на C++ можно следующим образом:

//============================================================================
// Name        : mkr.cpp
// Author      : 
// Version     :
// Copyright   : Your copyright notice
// Description :
//============================================================================

#include <iostream>
#include <cmath>
using namespace std;

double p(double x){
        return exp(x);
}

double q(double x){
        return 2*x;
}

double f(double x){
        return pow(x,3);
}

void gauss(double** A, double* B, double* X, int n);

int main() {
        double alpha0=2; double alpha1=-2.5; double Ac=0;
        double beta0=3; double beta1=-3.4; double Bc=5;
        double a0=0.1; double b0=1.3;
        int n=4;
        //matrix A[n+1][n+1]
        double **A = new double*[n+1];
        for(int i=0; i<n+1; i++){
                A[i]=new double[n+1];
        }
        //===
        double *B = new double[n+1]; //vector B[n+1]
        double *X = new double[n+1]; //vector X[n+1]
        //Grid
        double h=(b0-a0)/n;
        for(int i=0; i<=n; i++){
                X[i]=a0+i*h;
                //cout << X[i] << endl;
        }
        //===
        cout << "h=" << h << endl;
        //calculate matrix A, B
        for(int i=0; i<=n-2; i++){
        A[i][i]=h*h*q(X[i])-h*p(X[i])+1;
        A[i][i+1]=h*p(X[i])-2;
        A[i][i+2]=1;
        B[i]=h*h*f(X[i]);
        }
        A[n-1][0]=alpha0*h-alpha1;
        A[n-1][1]=alpha1;
        A[n][n-1]=-beta1;
        A[n][n]=beta0*h+beta1;
        B[n-1]=h*Ac;
        B[n]=h*Bc;
        //===
        //print A
        for(int i=0; i<=n; i++){
                for(int j=0; j<=n; j++){
                        cout << "A["<<i<<"]"<<"["<<j<<"]="<<A[i][j] <<" ";
                }
                cout << endl;
        }
        //===
        cout << endl;
        //print B
        for(int i=0; i<=n; i++){
                cout << "B["<<i<<"]="<<B[i] <<" ";
        }
        cout << endl;
        cout << endl;
        //===
        //solve A*X1=B
        double *X1 = new double[n+1]; //vector X1[n+1]
        gauss(A,B,X1,n+1); //solve
        //print X1
        for(int i=0; i<=n; i++){
                cout << "X1[" << i << "]=" << X1[i] << " ";
        }
        //===
        return 0;
}

void gauss(double** A, double* B, double* X, int n){
        int m=n+1;
        //create C[n][n+1]
        double **C = new double*[n];
        for(int i=0; i<n; i++){
                C[i]=new double[n+1];
        }
        //===
        //split A and B to C
        for(int i=0;i<n;i++){
                for(int j=0;j<n;j++){
                        C[i][j]=A[i][j];
                }
                C[i][n]=B[i];
        }
        //===
        /*
        //print C
        for(int i=0;i<n;i++){
                for(int j=0;j<n+1;j++){
                        cout << C[i][j] << " ";
                }
                cout << endl;
        }
        //===
        */

        //forward
        for (int k=0; k<n-1; k++){
            for (int i=k+1;i<n;i++){
                for (int j=m-1; j>=k; j--){
                        C[i][j]=C[i][j]-C[i][k]*C[k][j]/C[k][k];
                }
        }
        }
        //reverse
        X[n-1]=A[n-1][m-2]/A[n-1][m-2];

        for (int i=n-2; i>=0; i--){
                double s=0;
                for (int j=i+1;j<m-1;j++){
                        s=s+C[i][j]*X[j];
                }
                X[i]=(C[i][m-1] - s)/C[i][i];
        }

}