Пусть функция f(x) задана таблицей
x x0 x1 … xn
y y0 y1 … yn
Интерполяционным многочленом Лагранжа называется многочлен
Объявляем функцию для организации вычислений по формуле интерполяционного многочлена Лагранжа
def lagranz(x,y,t):
z=0
for j in range(len(y)):
p1=1; p2=1
for i in range(len(x)):
if i==j:
p1=p1*1; p2=p2*1
else:
p1=p1*(t-x[i])
p2=p2*(x[j]-x[i])
z=z+y[j]*p1/p2
return z
Пример. Написать программу для вычисления значений интерполяционного многочлена Лагранжа для функции, заданной таблицей
x 2 5 -6 7 4 3 8 9 1 -2
f(x) -1 77 -297 249 33 9 389 573 -3 -21
Решение
import numpy as np
import matplotlib.pyplot as plt
x=np.array([2,5,-6,7,4,3,8,9,1,-2], dtype=float)
y=np.array([-1,77,-297,249,33,9,389,573,-3,-21], dtype=float)
def lagranz(x,y,t):
z=0
for j in range(len(y)):
p1=1; p2=1
for i in range(len(x)):
if i==j:
p1=p1*1; p2=p2*1
else:
p1=p1*(t-x[i])
p2=p2*(x[j]-x[i])
z=z+y[j]*p1/p2
return z
xnew=np.linspace(np.min(x),np.max(x),100)
ynew=[lagranz(x,y,i) for i in xnew]
plt.plot(x,y,'o',xnew,ynew)
plt.grid(True)
plt.show()
Результат:
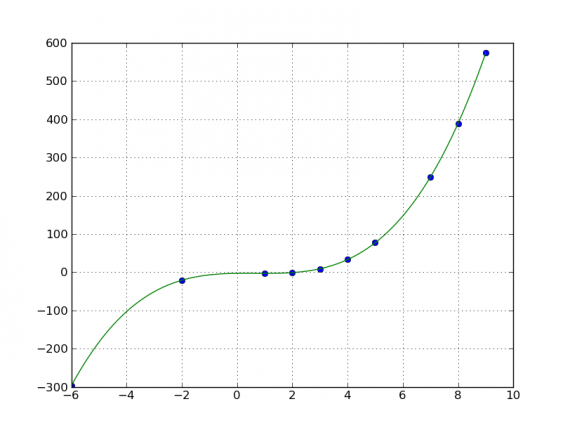
Для построения графика использовалась библиотека matplotlib. Некоторые примеры использования этой библиотеке можно посмотреть здесь:
